확률과 통계 - 베이즈 정리

베이즈 정리.

빅데이터 분석 기사 필기를 공부하면서 한번쯤은 들어본 내용이다.

그런데 이게 ML에서 중요하다고 하니 다시 공부해서 기록해본다...

 

---

우선,

 

빈도주의 vs 베이지안 주의

 

빈도주의는 과거의 기록을 바탕으로 증거를 내밀고, 베이지안 주의는 이 주장에 대한 신뢰?도가 몇인지를 표시한다.

즉 과거의 내가 동전을 100번 던졌는데, 50%가 앞면이 나왔어. - 빈도주의

 

동전의 앞면이 나올거야! 란 주장의 신뢰도는 50%야! - 베이지안 주의

---

쉽지 않다... 여튼 불확실성을 정량적으로 표현이 가능하다? 라고 생각한다.

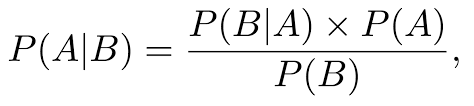
• P(A|B) : 사후확률 (posterior)
• P(B|A) : 우도or 가능도 (Likelihood)
• P(A) : 사전확률 (prior)

용어는 이렇게 된다... 나중에 ML에서 우도는 정말 중요해진다..우선은 용어까지만 보고..

여기서 왜 식이 저렇게 바뀌냐? 조건부 확률을 봐야한다.

조건부 확률을 보면 

출처 : heehehe's study note

이런 식이다. 즉 분자인 P(A∩B)이니 P(A)P(B|A)를 써준것이다.

 

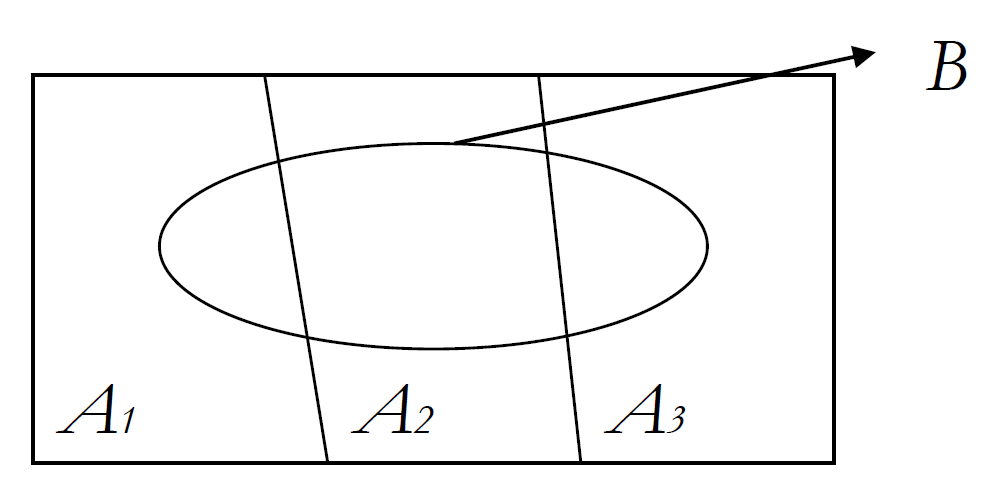
그렇다면 아래 이미지와 같은 상황에서

ratsgo'blog

P(B)는 A1,A2,A3의 교집합의 합과 같으니깐,

 

P(B)=P(A1∩B)+P(A2∩B)+P(A3∩B)

이것은 다시, P(B)=P(A1)P(B|A1)+P(A2)P(B|A2)+P(A3)P(B|A3)=∑P(A)P(B|A)

으로 표현이 가능하다.

 

 

수학식으로 어떻게 표현하는거야;; 

 

인용 글

 

1. https://angeloyeo.github.io/2020/01/09/Bayes_rule.html

베이즈 정리의 의미 - 공돌이의 수학정리노트

2. https://ratsgo.github.io/statistics/2017/07/01/bayes/

베이즈 규칙과 다양한 문제들 · ratsgo's blog

 

3. https://heehehe-ds.tistory.com/entry/%ED%86%B5%EA%B3%84%ED%95%99-6-4-%EB%B2%A0%EC%9D%B4%EC%A6%88-%EC%A0%95%EB%A6%AC